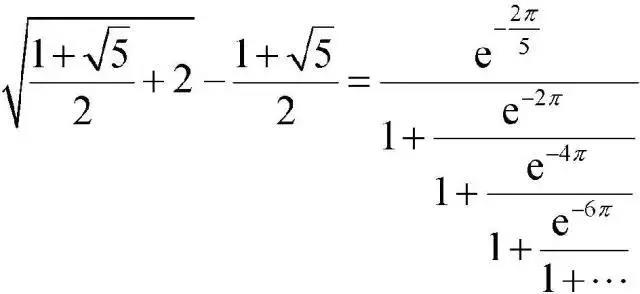据说，这是当今十大美丽的数学公式，快来选出你的最爱吧！叹为观止！

 

【Top 10】无名公式（好吧发现者似乎倾向于将其命名为姐妹公式）：这组公式是原贴作者发现的，具有惊人的镜像般的高度对称感，但作者表示考虑到之后九个的大神般存在，还是默默放到第十了。

 

 

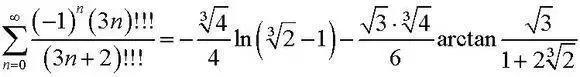
【Top 9】圆周率与自然对数底的近似关系式：能把圆周率和e联系起来的初等公式在数学界是少之又少，是数学王国中的国宝级公式。除了大名鼎鼎的欧拉公式，恐怕就是这个式子比较出名了。这个公式的形式异常的漂亮，只可惜它只是个近似公式。所以排名第九。虽然是个近似公式，但是近似程度相当的高，有七位有效数字是相同的，也就是说二者的差别在千万分之一以内。可以用电脑上的计算器一试。

 

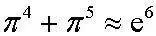
【Top 8】梅钦公式：熟悉圆周率计算方法的人应该对这个公式不陌生。这个公式的神奇之处在于它将圆周率表示为了两个分数的反正切之和。利用复数的指数表达式可以直接证明这个式子。它是历史上第一个用于快速计算圆周率的公式，因为上式中的反正切函数值可以被泰勒级数所逼近。真不知道如果祖冲之知道了这个计算圆周率的方法会埋头算到小数点后几百位……

 

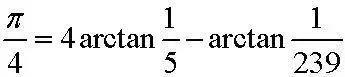
【Top 7】约翰-伯努利公式之一（只是传说是他发现的）：这个神奇的公式传说是约翰-伯努利发现的。式子的神奇之处就不用我说了吧，连续与离散的关系被表现得淋漓尽致。如果你自认为你的微积分水平还不错，可以挑战一下这个已经具有300多年历史的公式，看你能否证明它。

 

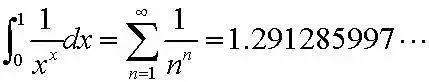
【Top 6】又是无名式：话说世人皆知勾三股四弦五，而鲜有知道这个简单等式的。这个简单的式子可以在英国分析学大师G·H·哈代（就是拉马努金在英国的合作者）所著的《数论导引》中找到，它是一类三次不定方程最简单的特解。

 

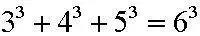
【Top 5】还是无名式：这个公式来自于印度数学奇才拉马努金。他曾经深入的研究了形如上式的无穷根式并得到了这个神奇的结果。传说拉马努金曾经把这个结果放在《印度数学会刊》上征集证明，结果数月内无人能应。各位看官有没有蠢蠢欲动的？ 

 

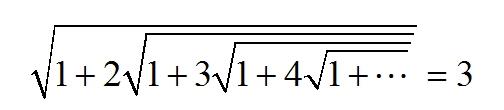
【Top 4】高斯公式之一：不消说，这个余弦特殊值足以说明：正十七边形是可以尺规作图的。在发现此式之前人们找到的、能用根式表达余弦值的角度大部分还停留在欧几里得时期的水平。高斯也因为他在19岁就做出的这项了不起的成果而开始从事数学研究。古典文学从此永远的失去了高斯。在作出这项告慰古希腊先贤们的贡献之后，小高斯就建立了一个自己的科学笔记，专门介绍自己最新的数学发现。 
 

 

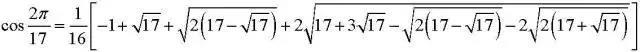
 【Top 3】扯淡忽悠人公式：这个貌似神奇的式子来自50多年前的《Scientific American》（其神奇之处在于它似乎把无理的e表达为有理了）。当时著名的趣味数学大师马丁·加德纳所主持的一个专栏上出现了这个公式，只可惜出版的当天日期是4月1号。这个式子或许可以蒙普通读者，但是绝对蒙不了数学家，因为根据著名的林德曼定理容易判定等式左边的e指数一定是一个超越数，绝对不可能是一个整数。然而如果你用mathematica去计算的话会惊奇的发现：这个超越数的值是：262537412640768743.9999999999992500725972……竟然有12个9！！即使如此它仍然是一个超越数，一种比无理数还“无理”的数……

 

 【Top 2】那就是受到我们万世敬仰的欧拉公式：上面欧拉公式的漂亮之处就不用我解释了吧。人们经常把它与老爱同志的E=mc^2并列为数学和物理学公式中的双子星。历史上的欧拉是一位全才数学家，同时也是一名虔诚的教徒，笃信上帝的存在。据说有一次俄国的叶卡捷琳娜二世邀请狄德罗来访问她的宫廷，而狄德罗是一名不折不扣的无神论者。不久叶卡捷琳娜二世就厌倦了狄德罗那喋喋不休的无神论说教之词，让欧拉来好好教训他一顿。欧拉开门见山的质问道：“e^i*pi+1=0（就是欧拉公式），所以上帝存在，请回答！”结果不懂数学的狄德罗被弄得一头雾水，无言以对。

  

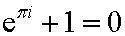
  【Top 1】拉马努金连分数公式 ：这个绝美的公式不仅像欧拉公式一样联系起了圆周率和e，同时它还将黄金分割数也包含在内！在1913年，来自南印度的小职员拉马努金，给当时32岁就已经执掌英国数学界牛耳的哈代去了一封长达9页的信，信中附带了120条拉马努金自己发现的公式，上面这个公式就是其中的一条。这条公式令哈代完全摸不到头脑，他这辈子都没见过这样的公式，连稍微接近点的都没有！但是哈代确信这个公式是对的，因为没有人能有这样的想象力去编造这样漂亮的公式。虽然不久之后，数学家们就严格的证明了这个式子，但是它和谐而又气势磅礴的形式令每一个初次见到它的人都会为之悸动！所以，拉马努金的这个公式绝对无愧于我们的最美数学公式榜首位置！