点击此链接可观看
http://open.sina.com.cn/course/id_1033/
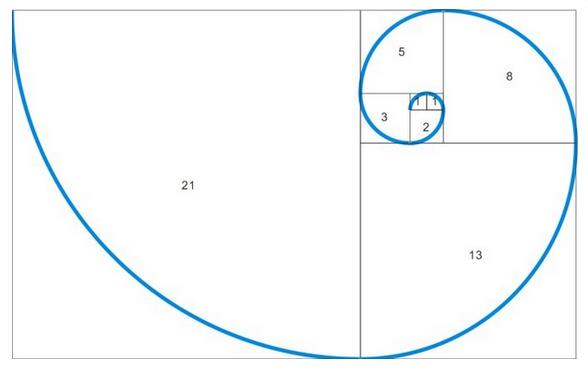
斐波那契数列,又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)在现代物理、准晶体结构、化学等领域,斐波那契数列都有直接的应用,为此,美国数学会从1963起出版了以《斐波那契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。

1.基本定义
斐波那契数列指的是这样一个数列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,......
这个数列从第2项开始,每一项都等于前两项之和。
斐波那契数列的发明者,是意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci),生于公元1170年,卒于1250年,籍贯是比萨。他被人称作“比萨的列昂纳多”。1202年,他撰写了《算盘全书》(Liber Abacci)一书。他是第一个研究了印度和阿拉伯数学理论的欧洲人。他的父亲被比萨的一家商业团体聘任为外交领事,派驻地点相当于今日的阿尔及利亚地区,列昂纳多因此得以在一个阿拉伯老师的指导下研究数学。他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯等地研究数学。
2.通项公式

3.斐波那契数列与黄金分割
有趣的是:这样一个完全是自然数的数列,通项公式却是用无理数来表达的。而且当n趋向于无穷大时,前一项与后一项的比值越来越逼近黄金分割0.618.(或者说后一项与前一项的比值小数部分越来越逼近黄金分割0.618、前一项与后一项的比值越来越逼近黄金分割0.618)
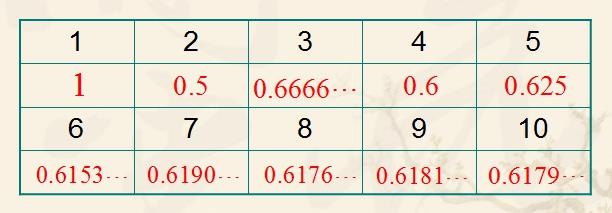
越到后面,这些比值越接近黄金比.
4.生活中的斐波那契数列
斐波那契数列中的斐波那契数会经常出现在我们的眼前——比如松果、凤梨、树叶的排列、某些花朵的花瓣数(典型的有向日葵花瓣),蜂巢,蜻蜓翅膀,超越数e(可以推出更多),黄金矩形、黄金分割、等角螺线,十二平均律等。
(1)花瓣的数目

(2) 植物种子的排列,类似的还有松子,花菜,菠萝等等.




(3) 树木的枝干

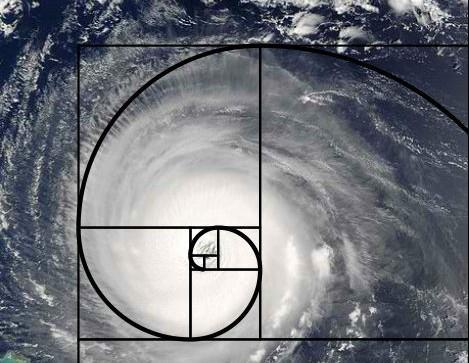
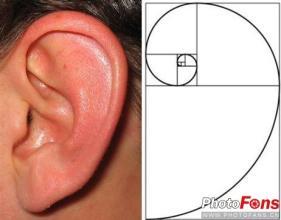
5.随处可见的斐波那契螺旋线