皮耶·德·费马(Pierre de Fermat)是一个17世纪的法国律师,也是一位业余数学家。之所以称业余,是由于皮耶·德·费马具有律师的全职工作。根据法文实际发音并参考英文发音,他的姓氏也常译为“费尔玛”(注意“玛”字)。费马最后定理在中国习惯称为费马大定理,西方数学界原名“最后”的意思是:其它猜想都证实了,这是最后一个。著名的数学史学家贝尔(E. T. Bell)在20世纪初所撰写的著作中,称皮耶·德·费马为“业余数学家之王”。贝尔深信,费马比皮耶·德·费马同时代的大多数专业数学家更有成就。17世纪是杰出数学家活跃的世纪,而贝尔认为费马是17世纪数学家中最多产的明星。

1.成长经历
幼年生活
费马(也译为“费尔玛”)1601年8月17日出生于法国南部图卢兹附近的博蒙·德·洛马涅。他的父亲多米尼克·费马在当地开了一家大皮革商店,拥有相当丰厚的产业,使得费马从小生活在富裕舒适的环境中。
费马的父亲由于富有和经营有道,颇受人们尊敬,并因此获得了地方事务顾问的头衔,但费马小的时候并没有因为家境的富裕而产生多少优越感。费马的母亲名叫克拉莱·德·罗格,出身穿袍贵族。多米尼克的大富与罗格的大贵族构筑了费马极富贵的身价。
学习时期
费马小时候受教于他的叔叔皮埃尔,受到了良好的启蒙教育,培养了他广泛的兴趣和爱好,对他的性格也产生了重要的影响。直到14岁时,费马才进入博蒙·德·洛马涅公学,毕业后先后在奥尔良大学和图卢兹大学学习法律。
2.个人成就
对解析几何的贡献
费马独立于勒奈·笛卡儿发现了解析几何的基本原理。
1629年以前,费马便着手重写公元前三世纪古希腊几何学家阿波罗尼奥斯失传的《平面轨迹》一书。他用代数方法对阿波罗尼奥斯关于轨迹的一些失传的证明作了补充,对古希腊几何学,尤其是阿波罗尼奥斯圆锥曲线论进行了总结和整理,对曲线作了一般研究。并于1630年用拉丁文撰写了仅有八页的论文《平面与立体轨迹引论》。
费马于1636年与当时的大数学家梅森、罗贝瓦尔开始通信,对自己的数学工作略有言及。但是《平面与立体轨迹引论》的出版是在费马去世14年以后的事,因而1679年以前,很少有人了解到费马的工作,而现在看来,费马的工作却是开创性的。
《平面与立体轨迹引论》中道出了费马的发现。他指出:“两个未知量决定的—个方程式,对应着一条轨迹,可以描绘出一条直线或曲线。”费马的发现比勒奈·笛卡儿发现解析几何的基本原理还早七年。费马在书中还对一般直线和圆的方程、以及关于双曲线、椭圆、抛物线进行了讨论。
笛卡儿是从一个轨迹来寻找它的方程的,而费马则是从方程出发来研究轨迹的,这正是解析几何基本原则的两个相对的方面。在1643年的一封信里,费马也谈到了他的解析几何思想。他谈到了柱面、椭圆抛物面、双叶双曲面和椭球面,指出:含有三个未知量的方程表示一个曲面,并对此做了进一步地研究。

1660年费玛的手稿之一
对微积分的贡献
16、17世纪,微积分是继解析几何之后的最璀璨的明珠。人所共知,牛顿和莱布尼茨是微积分的缔造者,并且在其之前,至少有数十位科学家为微积分的发明做了奠基性的工作。但在诸多先驱者当中,费马仍然值得一提。
曲线的切线问题和函数的极大、极小值问题是微积分的起源之一。这项工作较为古老,最早可追溯到古希腊时期。阿基米德为求出一条曲线所包任意图形的面积,曾借助于穷竭法。由于穷竭法繁琐笨拙,后来渐渐被人遗忘、直到16世纪才又被重视。由于约翰尼斯开普勒在探索行星运动规律时,遇到了如何确定椭圆形面积和椭圆弧长的问题,无穷大和无穷小的概念被引入并代替了繁琐的穷竭法。尽管这种方法并不完善,但却为自卡瓦列里到费马以来的数学家开辟厂一个十分广阔的思考空间。费马建立了求切线、求极大值和极小值以及定积分方法,对微积分做出了重大贡献。

对概率论的贡献
早在古希腊时期,偶然性与必然性及其关系问题便引起了众多哲学家的兴趣与争论,但是对其有数学的描述和处理却是15世纪以后的事。l6世纪早期,意大利出现了卡尔达诺等数学家研究骰子中的博弈机会,在博弈的点中探求赌金的划分问题。到了17世纪,法国的帕斯卡和费马研究了意大利的帕乔里的著作《摘要》,建立了通信联系,从而建立了概率学的基础。
费马考虑到四次赌博可能的结局有2×2×2×2=16种,除了一种结局即四次赌博都让对手赢以外,其余情况都是第一个赌徒获胜。费马此时还没有使用概率一词,但他却得出了使第一个赌徒赢得概率是15/16,即有利情形数与所有可能情形数的比。这个条件在组合问题中一般均能满足,例如纸牌游戏,掷银子和从罐子里模球。其实,这项研究为概率的数学模型一概率空间的抽象奠定了博弈基础,尽管这种总结是到了1933年才由柯尔莫戈罗夫作出的。
费马和布莱士·帕斯卡在相互通信以及著作中建立了概率论的基本原则——数学期望的概念。这是从点的数学问题开始的:在一个被假定有同等技巧的博弈者之间,在一个中断的博弈中,如何确定赌金的划分,已知两个博弈者在中断时的得分及在博弈中获胜所需要的分数。费马这样做出了讨论:一个博弈者A需要4分获胜,博弈者B需要3分获胜的情况,这是费马对此种特殊情况的解。因为显然最多四次就能决定胜负。
一般概率空间的概念,是人们对于概念的直观想法的彻底公理化。从纯数学观点看,有限概率空间似乎显得平淡无奇。但一旦引入了随机变量和数学期望时,它们就成为神奇的世界了。费马的贡献便在于此。
对数论的贡献
17世纪初,欧洲流传着公元三世纪古希腊数学家丢番图所写的《算术》一书。l621年费马在巴黎买到此书,他利用业余时间对书中的不定方程进行了深入研究。费马将不定方程的研究限制在整数范围内,从而开始了数论这门数学分支。
费马在数论领域中的成果是巨大的,其中主要有:
费马大定理:n>2是整数,则方程x^n+y^n=z^n没有满足xyz≠0的整数解。这个是不定方程,它已经由英国数学家怀尔斯证明了(1995年),证明的过程是相当艰深的!


费马小定理:a^p-a≡0(mod p),其中p是一个素数,a是正整数,它的证明比较简单。事实上它是Euler定理的一个特殊情况,Euler定理是说:a^φ(n)-1≡0(mod n),a,n都是正整数,φ(n)是Euler函数,表示和n互素的小于n的正整数的个数(它的表达式欧拉已经得出,可以在“Euler公式”这个词条里找到)。
另外还有:
(1)全部大于2的素数可分为4n+1和4n+3两种形式。
(2)形如4n+1的素数能够,而且只能够以一种方式表为两个平方数之和。
(3)没有一个形如4n+3的素数,能表示为两个平方数之和。
(4)形如4n+1的素数能够且只能够作为一个直角边为整数的直角三角形的斜边;4n+1的平方是且只能是两个这种直角三角形的斜边;类似地,4n+1的m次方是且只能是m个这种直角三角形的斜边。
(5)边长为有理数的直角三角形的面积不可能是一个平方数。
(6)4n+1形的素数与它的平方都只能以一种方式表达为两个平方数之和;它的3次和4次方都只能以两种表达为两个平方数之和;5次和6次方都只能以3种方式表达为两个平方数之和,以此类推,直至无穷。
(7)发现了第二对亲和数:17296和18416。
十六世纪,已经有人认为自然数里就仅有一对亲和数:220和284。有一些无聊之士,甚至给亲和数抹上迷信色彩或者增添神秘感,编出了许许多多神话故事。还宣传这对亲和数在魔术、法术、占星术和占卦上都有重要作用等等。
距离第一对亲和数诞生2500多年以后,历史的车轮转到十七世纪,1636年,法国“业余数学家之王”费马找到第二对亲和数17296和18416,重新点燃寻找亲和数的火炬,在黑暗中找到光明。两年之后,“解析几何之父”——法国数学家勒奈·笛卡儿(René Descartes)于1638年3月31日也宣布找到了第三对亲和数9437506和9363584。费马和笛卡尔在两年的时间里,打破了二千多年的沉寂,激起了数学界重新寻找亲和数的波涛。
3.个人评价
费马一生从未受过专门的数学教育,数学研究也不过是业余之爱好。然而,在17世纪的法国还找不到哪位数学家可以与之匹敌:他是解析几何的发明者之一;对于微积分诞生的贡献仅次于艾萨克·牛顿、戈特弗里德·威廉·凡·莱布尼茨,他还是概率论的主要创始人,以及独撑17世纪数论天地的人。此外,费马对物理学也有重要贡献。一代数学天才费马堪称是17世纪法国最伟大的数学家。

谷歌纪念
2011年8月17日,GOOGLE的LOGO又更新了,这次的比较有意思,LOGO的标签上写着:“我发现了一个美妙的关于这个定理的证法 ,可惜这里地方太小,写不下。”这次谷歌(GOOGLE)的LOGO是纪念业余数学家之王--皮耶·德·费马的诞辰410周年。其实LOGO里的标签是揶揄他说的那句话:“我确信已找到了一个极佳的证明,但书的空白太窄,写不下。”
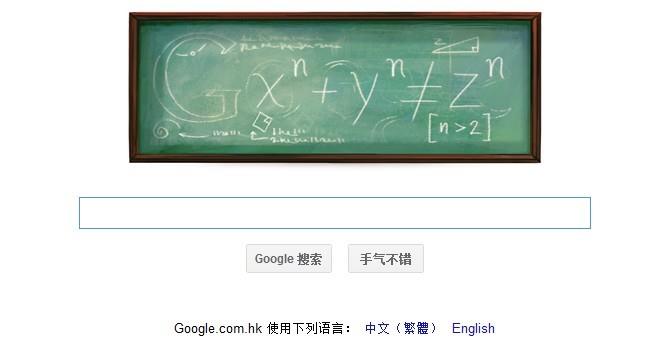
我发现了一个美妙的关于这个定理的证法 ,可惜这里地方太小,写不下。--皮耶·德·费马